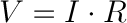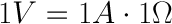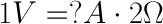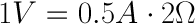Electrical Resistance and Ohm’s Law

Fundamental terms and Law in electronics Electrical Resistance and Ohm’s Law

Resistance is a measure of the opposition to current flow in an electrical circuit. Resistance is measured in ohms.

Considering the same example we used in previous topic i.e. two water tanks, one with a narrow pipe and one with a wide pipe.

The tank with the narrow pipe creates a higher resistance.

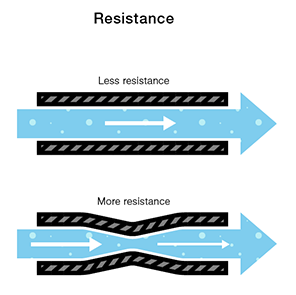
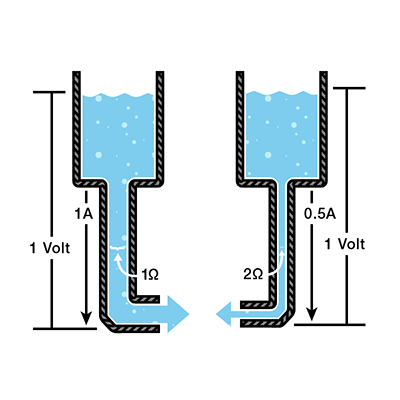
It stands to reason that we can’t fit as much volume through a narrow pipe than a wider one at the same pressure. This is resistance. The narrow pipe “resists” the flow of water through it even though the water is at the same pressure as the tank with the wider pipe.

In electrical terms, this is represented by two circuits with equal voltages and different resistances. The circuit with the higher resistance will allow less charge to flow, meaning the circuit with higher resistance has less current flowing through it.

Ohm’s Law

Combining the elements of voltage, current, and resistance, Ohm developed the formula:

Where

V = Voltage in volts
I = Current in amps
R = Resistance in ohms

This is called Ohm’s law. For example, a circuit with the potential of 1 volt, a current of 1 amp, and resistance of 1 ohm. Using Ohm’s Law we can say:

Let’s say this represents our tank with a wide hose. The amount of water in the tank is defined as 1 volt and the “narrowness” (resistance to flow) of the hose is defined as 1 ohm. Using Ohms Law, this gives us a flow (current) of 1 amp.

Using this analogy, let’s now look at the tank with the narrow hose. Because the hose is narrower, its resistance to flow is higher. Let’s define this resistance as 2 ohms. The amount of water in the tank is the same as the other tank, so, using Ohm’s Law, our equation for the tank with the narrow hose is

But what is the current? Because the resistance is greater, and the voltage is the same, this gives us a current value of 0.5 amps:

Tanks with their equivalent electrical meanings.

So, the current is lower in the tank with higher resistance. Now we can see that if we know two of the values for Ohm’s law, we can solve for the third.

Back to Lesson